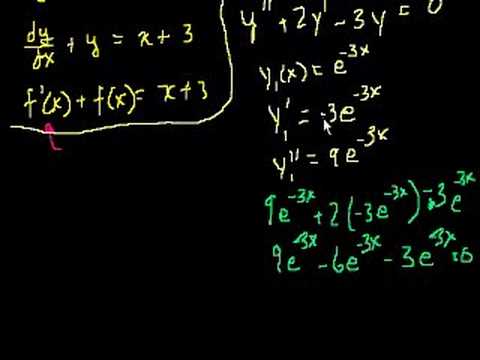Courses tagged with "Navigation+SAP" (27)
2. Dereceden Eşitsizliklerle ilgili bilmeniz gereken her şeyi bu derste bulacaksınız.
Videos on a first course in calculus (Differential Calculus).
Videos on a second course in calculus (Integral Calculus).
Calculus One is a first introduction to differential and integral calculus, emphasizing engaging examples from everyday life.
Sal works through the problems from the CA Standards.
Sal works through 80 questions taken from the California Standards Test for Algebra II.
Sal does the 80 problems from the released questions from the California Standards Test for Geometry.
Lecture Series on Mathematics - III by Prof.P.N.Agarwal, Department of Mathematics, IIT Roorkee.
Lectures by Prof. S.K.RayrnDepartment of Mathematics and StatisticsrnIIT Kanpur
Lectures by P.B.Sunil Kumar, Department of Physics, IIT Madras
In this course, you will look at the properties behind the basic concepts of probability and statistics and focus on applications of statistical knowledge. You will learn about how statistics and probability work together. The subject of statistics involves the study of methods for collecting, summarizing, and interpreting data. Statistics formalizes the process of making decisions, and this course is designed to help you use statistical literacy to make better decisions. Note that this course has applications for the natural sciences, economics, computer science, finance, psychology, sociology, criminology, and many other fields. We read data in articles and reports every day. After finishing this course, you should be comfortable evaluating an author's use of data. You will be able to extract information from articles and display that information effectively. You will also be able to understand the basics of how to draw statistical conclusions. This course will begin with descriptive statistic…
Topics covered in a first year course in differential equations. Need to understand basic differentiation and integration from Calculus playlist before starting here. What is a differential equation. Separable Differential Equations. Separable differential equations 2. Exact Equations Intuition 1 (proofy). Exact Equations Intuition 2 (proofy). Exact Equations Example 1. Exact Equations Example 2. Exact Equations Example 3. Integrating factors 1. Integrating factors 2. First order homegenous equations. First order homogeneous equations 2. 2nd Order Linear Homogeneous Differential Equations 1. 2nd Order Linear Homogeneous Differential Equations 2. 2nd Order Linear Homogeneous Differential Equations 3. 2nd Order Linear Homogeneous Differential Equations 4. Complex roots of the characteristic equations 1. Complex roots of the characteristic equations 2. Complex roots of the characteristic equations 3. Repeated roots of the characteristic equation. Repeated roots of the characteristic equations part 2. Undetermined Coefficients 1. Undetermined Coefficients 2. Undetermined Coefficients 3. Undetermined Coefficients 4. Laplace Transform 1. Laplace Transform 2. Laplace Transform 3 (L{sin(at)}). Laplace Transform 4. Laplace Transform 5. Laplace Transform 6. Laplace Transform to solve an equation. Laplace Transform solves an equation 2. More Laplace Transform tools. Using the Laplace Transform to solve a nonhomogeneous eq. Laplace Transform of : L{t}. Laplace Transform of t^n: L{t^n}. Laplace Transform of the Unit Step Function. Inverse Laplace Examples. Laplace/Step Function Differential Equation. Dirac Delta Function. Laplace Transform of the Dirac Delta Function. Introduction to the Convolution. The Convolution and the Laplace Transform. Using the Convolution Theorem to Solve an Initial Value Prob.
Topics covered in a first year course in differential equations.
Calculus can be thought of as the mathematics of CHANGE. Because everything in the world is changing, calculus helps us track those changes. Algebra, by contrast, can be thought of as dealing with a large set of numbers that are inherently CONSTANT. Solving an algebra problem, like y = 2x + 5, merely produces a pairing of two predetermined numbers, although an infinite set of pairs. Algebra is even useful in rate problems, such as calculating how the money in your savings account increases because of the interest rate R, such as Y = X0+Rt, where t is elapsed time and X0 is the initial deposit. With compound interest, things get complicated for algebra, as the rate R is itself a function of time with Y = X0 + R(t)t. Now we have a rate of change which itself is changing. Calculus came to the rescue, as Isaac Newton introduced the world to mathematics specifically designed to handle those things that change. Calculus is among the most important and useful developments of human thought. Even though it is over…
This course is the second installment of Single-Variable Calculus. In Part I (MA101) [1], we studied limits, derivatives, and basic integrals as a means to understand the behavior of functions. In this course (Part II), we will extend our differentiation and integration abilities and apply the techniques we have learned. Additional integration techniques, in particular, are a major part of the course. In Part I, we learned how to integrate by various formulas and by reversing the chain rule through the technique of substitution. In Part II, we will learn some clever uses of substitution, how to reverse the product rule for differentiation through a technique called integration by parts, and how to rewrite trigonometric and rational integrands that look impossible into simpler forms. Series, while a major topic in their own right, also serve to extend our integration reach: they culminate in an application that lets you integrate almost any function you’d like. Integration allows us to calculat…
Multivariable Calculus is an expansion of Single-Variable Calculus in that it extends single variable calculus to higher dimensions. You may find that these courses share many of the same basic concepts, and that Multivariable Calculus will simply extend your knowledge of functions to functions of several variables. The transition from single variable relationships to many variable relationships is not as simple as it may seem; you will find that multi-variable functions, in some cases, will yield counter-intuitive results. The structure of this course very much resembles the structure of Single-Variable Calculus I and II. We will begin by taking a fresh look at limits and continuity. With functions of many variables, you can approach a limit from many different directions. We will then move on to derivatives and the process by which we generalize them to higher dimensions. Finally, we will look at multiple integrals, or integration over regions of space as opposed to intervals. The goal of Mu…
If you invest in financial markets, you may want to predict the price of a stock in six months from now on the basis of company performance measures and other economic factors. As a college student, you may be interested in knowing the dependence of the mean starting salary of a college graduate, based on your GPA. These are just some examples that highlight how statistics are used in our modern society. To figure out the desired information for each example, you need data to analyze. The purpose of this course is to introduce you to the subject of statistics as a science of data. There is data abound in this information age; how to extract useful knowledge and gain a sound understanding in complex data sets has been more of a challenge. In this course, we will focus on the fundamentals of statistics, which may be broadly described as the techniques to collect, clarify, summarize, organize, analyze, and interpret numerical information. This course will begin with a brief overview of the discipline of stat…
Differential equations are, in addition to a topic of study in mathematics, the main language in which the laws and phenomena of science are expressed. In basic terms, a differential equation is an expression that describes how a system changes from one moment of time to another, or from one point in space to another. When working with differential equations, the ultimate goal is to move from a microscopic view of relevant physics to a macroscopic view of the behavior of a system as a whole. Let’s look at a simple differential equation. Based on previous math and physics courses, you know that a car that is constantly accelerating in the x-direction obeys the equation d2x/dt2 = a, where a is the applied acceleration. This equation has two derivations with respect to time, so it is a second-order differential equation; because it has derivations with respect to only one variable (in this example, time), it is known as an ordinary differential equation, or an ODE. Let’s say that we want to sol…
Trusted paper writing service WriteMyPaper.Today will write the papers of any difficulty.